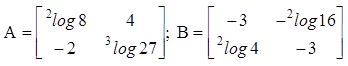SOAL DAN PEMBAHASAN KESAMAAN MATRIKS

Dua atau lebih matriks dikatakan sama bila memiliki ordo (jumlah baris dan kolom) sama dan komponen yang sama di setiap selnya. Dengan kata lain, matriks-matriks tersebut adalah matriks yang sama hanya saja dengan nama berbeda.

Prinsip kesamaan matriks pada umumnya digunakan untuk menentukan komponen pada sel tertentu atau menentukan variabel yang terdapat dalam komponen penyusun matriks.

Prinsip kesamaan matriks umumnya dihubungkan dengan persamaan matematika lainnya seperti persamaan linear dua variabel, persamaan kuadrat, eksponensial, logaritma, ataupun trigonometri.

Konsep Kesamaan Matriks

Bila dua matriks di atas dinyatakan sama, maka berlaku :
a = p; b = q; c = r
d = s; e = t; f = u
g = v; h = w; l = x

Kumpulan Soal

1. Jika diketahui matriks A dan B seperti di bawah ini, maka tentukanlah hubungan antara B + A dan A + B.
   
   

   

   
   

   Pembahasan :
   Sudah sangat jelas bahwa pada operasi penjumlahan matriks berlaku sifat komutatif sehingga B + A = A + B.
   
   
2. Sebuah matriks P ordo 2 x 2 memenuhi persamaan seperti di bawah ini, tentukanlah matriks P.
   
   

   

   Pembahasan :
   Misalkan elemen-elemen matriks P adalah a, b, c, dan d
   
   

   

   
   7 - 3a = -5  ---> -3a = -12 ---> a = 4
   1 - 3b = 10 ---> -3b = 9 ---> b = -3
   -4 - 3c = 8 ---> -3c = 12 ---> c = -4
   3 - 3d = 9 ---> -3d = 6 ---> d = -2
   
   Jadi matriks P adalah :
   

   

   
   

   
   
   
3. Tentukanlah nilai x dan z yang memenuhi persamaan matriks berikut ini :
   
   

   

   Pembahasan :
   -1 + 6 = 2 + 2x
   5 = 2 + 2x
   3 = 2x
   x = 3/2
   
   3 + 2 = 3 + z + 1
   5 = 4 + z
   z = 1
   
   
4. Tentukan besar sudut a dan sudut b.
   
   

   

   Pembahasan :
   cos a = 2 + (-2) = 0 ---> a = 90
   sin b = 3 + (2,5) = 0,5 = 1/2 ---> b = 30
   
   
5. Diketahui persamaan matriks sebagai berikut :
   
   

   

   Tentukanlah nilai a, b, c, dan d.
   
   Pembahasan :
   -a + 3 = 10 ---> a = -7
   
   c - 2 + 10 = -6
   c = - 6 - 8
   c = -14
   
   b + 4 + b + c = -6
   2b + c = -10
   2b - 14 = -10
   2b = 4
   b = 2
   
   2d + d = b - 2
   3d = 2 - 2
   d = 0
   
   
6. Berdasarkan persamaan matriks di bawah ini, tentukanlah nilai a, b, c, dan d.
   
   

   

   Pembahasan :
   2d + d = -2 + (-4)
   3d = -6
   d = -2
   
   a + 2d + 3 = 10 + 2
   a + 2(-2) = 12 - 3
   a - 4  = 9
   a = 9 + 4
   a = 13
   
   b + b + 3c = 16 + 8
   2b + 3c = 24
   
   c - 2 + 2 + b = -6 + 6
   c + b = 0 ---> c = -b ---> substitusi ke persamaan 2b + 3c = 24
   2b + 3(-b) = 24
   2b - 3b = 24
   -b = 24
   b = -24 maka c = 24
   
   Jadi a = 13. b = -24, c = 24, dan d = -2
   
   

   
   
   
7. Jika p, q, r, dan s memenuhi persamaan matriks 
   
   

   

   Pembahasan :
   Dari soal, diperoleh 4 persamaan yaitu :
   1. p - 2s = 1
   2. 2q - r = 1
   3. 2r - q = -1
   4. s - 2p = -1
   
   Dari persamaan no 1 dan 4 diperoleh :
   p - 2s = 1 ---> p = 1 + 2s ---> substitusikan ke persamaan 4
   s - 2p = -1
   s - 2(1 + 2s) = -1
   s - 2 - 4s = -1
   -3s = 1
   s = -1/3
   
   selanjutnya,
   p - 2(-1/3) = 1
   p + 2/3 = 1
   p = 1 - 2/3 = 1/3
   
   Dari persamaan no 2 dan 3 diperoleh :
   2q - r = 1 ---> -r = 1 - 2q ---> r = 2q + 1 ---> substitusi ke persamaan 3
   2r - q = -1
   2(2q + 1) - q = -1
   4q + 2 - q = -1
   3q = -3
   q = -1
   
   selanjutnya,
   2(-1) - r = 1
   -r = 1 + 2 = 3
   r = -3
   
   Jadi p = 1/3, q = -1, r = -3 , dan s = -1/3
   
   
8. Tentukan nilai x yang memenuhi persamaan matriks di bawah ini.
   
   

   

   Pembahasan :
   Dari hubungan di atas, diperoleh
   log (2a - 2) = 1
   log (2a - 2) = log 10
   2a - 2 = 10
   a = 12/2 = 6
   
   log (b-4) = log a
   log (b-4) = log 6
   b-4 = 6
   b = 10
   
   ^xlog a = log b
   ^xlog 6 = log 10
   ^xlog 6 = 1
   x = 6
   
   Jadi nilai x yang memenuhi persamaan di atas adalah 6
   
   
9. Tentukan nilai a
   
   

   

   Pembahasan :
   a + 3ab + a² = a - 2
   a - a + 3ab + a² + 2 = 0
   a² + 3ab + 2 = 0  ---> persamaan kuadrat
   
   Agar persamaan di atas dapat diselesaikan, kita cari nilai b terlebih dahulu.
   b + 4 + b = 6
   2b = 6 - 4
   b = 2/2 = 1
   
   Persamaan kuadrat di atas menjadi :
   a² + 3a + 2 = 0
   (a + 2) (a + 1) = 0
   a = -2   atau  a = -1
   
   
10. Tentukan hubungan matriks A dan B jika diketahui
    
    

    

    Pembahasan :
    Karena soal ini termasuk pada bab kesamaan matriks, maka anggaplah bahwa A = nB, dengan n adalah suatu bilangan tertentu yang menjelaskan hubungan keduanya.
    
    

    

    Dari hubungan di atas, agar bernilai sama maka nilai n = -1
    maka A = -B

Advertiser